
4.アルゴリズム基礎
突然アルゴリズムという聞きなれない言葉が出てきました(最近はアルゴリズム体操なんかでメジャーな言葉なんでしょうか?).三省堂の『大辞林 』によると,

一見して四輪の花が咲いていることが分かります.それでは,これらの四輪の花の位置を求める方法を考えましょう.紫色の画素は花1から花4のどれかに属していると考えることができます.つまり全ての紫色の画素は4つの花の固まりのどれかに分類することができる訳ですが,このような作業をクラスタリングといいます.そして,一つ一つの固まり(花)のことをクラスタと呼びます.
画像認識ではこのようなクラスタリング問題を扱うことが非常に多く,その最も単純な方法が k−平均アルゴリズム(k−平均法)です.人間にとってはとても簡単なクラスタリング問題でも,いざコンピュータに解かせるとなると難しいことが多いです.このような問題を解決するための計算手続きをアルゴリズムといいます.
さて,k−平均法の k とは何でしょうか.それはクラスタの数を意味しています.つまりこの問題では4です.k−平均法は k の数が分かった時に(今回は k = 4 ),それらのクラスタの中心を求める方法ということができます.
アルゴリズムは非常にシンプルです.まず初期値としてそれぞれのクラスタ中心を適当に与えます.今回のクラスタ数は4なので,四隅の座標を与えましょう.そして bin4.ppm の紫の画素において,どのクラスタに最も近いかを調べます.ここでは下図左のようにクラスタ0に近い画素を赤色,クラスタ1に近い画素を緑色,クラスタ2に近い画素を青色,クラスタ3に近い画素を紫色で表示します.次にそれぞれの色の中心座標を求めます.それが下図の中央です.クラスタ中心が動いていますね.
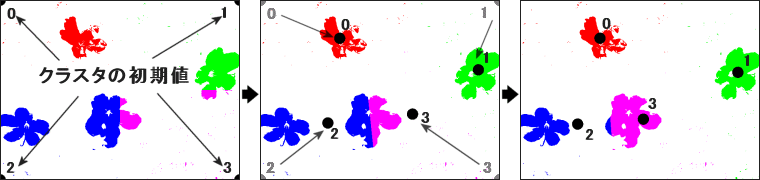
再び新しく求めたクラスタ中心に対して同じ作業を繰り返します.そうすると徐々に正解クラスタに近づいていき,クラスタ中心は動かなくなってきます.そうすれば打ち切りです.今回の場合は5〜6回繰り返せば,下図右画像のように正しい結果に収束します.

最終的に収束したクラスタの座標を出力すれば,画像上での四輪の花の位置を知ることができます.それでは k−平均法をプログラムしてみましょう.大枠は下に示してありますので,何をしているのかをよく考えながら完成させて下さい.
#define K 4
//ppm ファイルを書き込む関数(画像サイズは640×480のみ対応)
int ppm_write(char *filename, unsigned char *pimage){
FILE *fp;
fp=fopen(filename,"wb");
fprintf(fp,"P6\n640 480\n255\n");
fwrite(pimage,sizeof(char),640*480*3,fp);
fclose(fp);
return 0;
}
struct cluster{ //クラスタを表す構造体
float now_x, now_y; //現在のクラスタの中心
int no; //クラスタに属する画素の数
float new_x, new_y; //反復計算で求めるクラスタ中心
};
float dis(struct cluster cluster, int x, int y){
// (cluster.now_x, cluster.now_y) と (x,y) の距離を求める関数
float d;
d = sqrt( (cluster.now_x - x)*(cluster.now_x - x) + (cluster.now_y - y)*(cluster.now_y - y) );
return d;
}
main(){
unsigned char image[480][640][3]; //取り込む画像
unsigned char image2[480][640][3]; //結果の画像
int x,y,i;
int loop;
char filename[64];
struct cluster cluster[K]; //クラスタ情報
for( i=0 ; i < K ; i++){ //初期化
cluster[i].new_x = cluster[i].new_y = cluster[i].no = 0;
}
//初期値は適当に与える(今回は四隅にする)
cluster[0].now_x = 0; cluster[0].now_y = 0;
cluster[1].now_x = 639; cluster[1].now_y = 0;
cluster[2].now_x = 0; cluster[2].now_y = 479;
cluster[3].now_x = 639; cluster[3].now_y = 479;
ppm_read("bin3.ppm", &image[0][0][0]); //ファイルの読み込み
for( loop = 0 ; loop < 10 ; loop++ ){ //今回は収束判定はせずに10回で打ち切り
for( y=0 ; y<480 ; y++ ){
for( x=0 ; x<640 ;x++ ){
image2[y][x][0] = 0xff; image2[y][x][1] = 0xff; image2[y][x][2] = 0xff; //まずは白色に
if( image[y][x][0] == 0xff && image[y][x][1] == 0x00 && image[y][x][2] == 0xff ){
//紫色の画素はクラスタリング対象
if( dis(cluster[0],x,y) < dis(cluster[1],x,y) &&
dis(cluster[0],x,y) < dis(cluster[2],x,y) &&
dis(cluster[0],x,y) < dis(cluster[3],x,y) ){ //(x,y) は cluster[0] に最も近い
image2[y][x][0] = 0xff; image2[y][x][1] = 0x00; image2[y][x][2] = 0x00; //途中結果を赤で塗る
cluster[0].no++; // 平均を求めるために記憶する
cluster[0].new_x+=x;
cluster[0].new_y+=y;
}
else if(){... すべてのクラスタに関して同様の処理
}
}
// クラスタ中心に●を書く
for( i=0 ; i < K ; i++){
if( dis(cluster[i],x,y) < 15 ){
image2[y][x][0] = 0x00; image2[y][x][1] = 0x00; image2[y][x][2] = 0x00; //黒色に
}
}
}
}
for( i=0 ; i < K ; i++ ){ //クラスタ平均を求める
cluster[i].now_x = cluster[i].new_x/cluster[i].no; //新しいクラスタ中心
cluster[i].now_y = cluster[i].new_y/cluster[i].no;
cluster[i].new_x = cluster[i].new_y = cluster[i].no = 0; //初期化
}
sprintf(filename, "result_%d.ppm",loop);
ppm_write(filename, &image2[0][0][0]); // 結果のファイルを書き出す
}
}
|
 演習4−1
演習4−1

また,演習で考えてもらったk−平均アルゴリズムでクラスタリングが難しい例は下図のようなものがあります.クラスタ中心からの距離によってクラスタリングをしているため,横に長い棒のようなものをクラスタリングするのは難しいという欠点があります.一例を muri.ppm に示します.bin?.ppm と同じフォーマットになっていますので,実際に処理して確認しましょう.

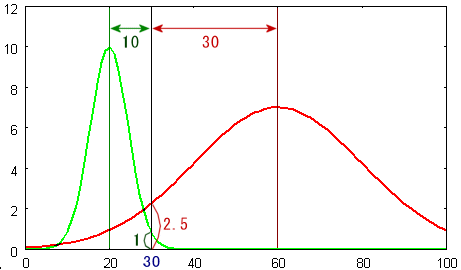
k−平均法においてクラスタは平均値のみで表現されていました.しかし,クラスタが統計的な性質を持つ場合には平均値だけではなく,分散値も考慮する方がよい結果が得られると思われます.例えば下図のような分布を考えてみましょう.今までは2次元平面上でのクラスタリングを考えてきましたが,ここからは問題を簡単にするために一次元の数直線上でのクラスタリングを考えることにします.
緑の分布がクラスタ1,赤の分布がクラスタ2だとします.クラスタ1の中心(平均)は20,クラスタ2の中心(平均)は60であることはすぐに分かります.この時に30という値があった場合に,これはクラスタ1のものでしょうか?それとも2のものでしょうか? k−平均法のように中心からの距離によって判断するとクラスタ1の方が近いためクラスタ1に属してしまいます.しかし,このグラフを見ると30はクラスタ2である可能性が高いと思われます.もっというと,クラスタ1である可能性は 1/(1+2.5),クラスタ2である可能性は 2.5/(1+2.5) であることが分かると思います.
このように平均だけではなく,分散も考慮したクラスタリング問題はEMアルゴリズムによって解くことができます.
ただ,この先は執筆中です….完成はいつになるかは分かりません.気長にお待ち下さい.